Компьютерная логика (тест с ответами): Представление данных в вычислительной системе.

31 18

1). (из 18): Укажите чему равно десятичное значение упакованного BCD числа 1001 0101 0011 1101:

а) -2387;

б) 953;

в) 38205;

г) -38205;

д) -953; +

е) сложный вопрос;

2). (из 18): Укажите чему равно десятичное значение неупакованного BCD числа 0011 0010 0010 0011 0011 0100 0011 0101:

а) -2345;

б) 2345;

в) 842216661;

г) -842216661;

д) -52638533;

е) 52638533;

ж) формат неупакованного BCD числа представлен неверно; +

3). (из 18): Если тип данных, предназначенный для работы с числами с плавающей запятой имеет 10 разрядов для хранения смещённого порядка, то смещение в данном случае будет равно:

а) 511; +

б) 512;

в) 2048;

г) 2047;

д) -511;

е) -512;

ж) -2048;

з) -2047;

4). (из 18): Представить число -2835,625 в машинном виде с использованием 4 байтного представления (где 1 бит отводится под знак числа, 10 бит - под смещённый порядок, остальные биты - под мантиссу). Принцип скрытой единицы не используется.

а) 1100 0001 0110 0000 0101 1000 1001 1101;

б) 0100 0001 0111 0110 0010 0111 0100 0000;

в) 1100 0001 0111 0110 0010 0111 0100 0000; +

г) 0100 0001 0110 0000 0101 1000 1001 1101;

д) 1100 0001 0110 0000 0001 1000 1001 1101;

5). (из 18): Представить число 96452,1345 в машинном виде с использованием 5 байт(1 бит-под знак числа,13 бит-под смещённый порядок,остальные биты-под мантису). Принцип скрытой единицы используется. Если вычисляемое число невозможно точно представить в двоичной системе,то получите 10 знаков после запятой:

а) 0100 0000 0100 0010 1111 0001 1000 1000 0100 0100;

б) 1100 0000 0100 0010 1111 0001 1000 1000 0100 0100;

в) 0100 0000 0001 1100 1111 0001 1000 1000 0100 0100 1000;

г) 0100 0000 0011 1101 1110 0011 0001 0000 1000 1000;

д) 0100 0000 0011 1101 1110 0011 0001 0000 1000 1001; +

е) 0100 0000 0001 1100 1111 0001 1000 1000 0100 01001;

6). (из 18): Представить число -3547235, записанное в форме с фиксированной запятой, в машинном виде с использованием 4-ёх байтного представления со знаком:

а) 1110 1100 0100 0000 1100 0110 0000 0000;

б) 1000 0000 0011 0110 0010 0000 0110 0011; +

в) 0000 0000 0011 0110 0010 0000 0110 0011;

г) 0110 1100 0100 0000 1100 0110 0000 0000;

д) 1101 1011 0110 0010 0000 0110 0011 0000;

е) 1000 1100 0110 0000 0100 0110 1101 1011;

7). (из 18): Из кода действительного числа, представленного в машинном виде как ABC6328010000000, получить десятичное представление этого числа, учитывая, что принцип скрытой единицы используется. Тип DOUBLE:

а) -0,693664580583572*10^(-322*ln(2)/ln(10)); +

б) 0,387329161167145*2^323;

в) 0,387329161167145*10^(323*ln(2)/ln(10));

г) 0,693664580583572*2^(322);

д) -0,693664580583572*2^(-322); +

е) 0,693664580583572*2^(-322);

ж) 0,693664580583572*10^(-323*ln(2)/ln(10));

8). (из 18): Из кода действительного числа, представленного в машинном виде как F00AB0C0, получить десятичное представление этого числа, учитывая, что принцип скрытой единицы используется. Тип SINGLE:

а) -0,083518981933593700*2^(97);

б) -0,083518981933593700*10^(97*ln(2)/ln(10));

в) 0,083518981933593700*2^(97);

г) -0,083518981933593700*10^(-97*ln(2)/ln(10));

д) 0,541759490966796*2^(98);

е) -0,541759490966796*2^(98); +

ж) -0,541759490966796*10^(98*ln(2)/ln(10)); +

з) 0,541759490966796*10^(98*ln(2)/ln(10));

9). (из 18): Из кода действительного числа, представленного в машинном виде как 105FABC6328100000000, получить десятичное представление этого числа, учитывая, что принцип скрытой единицы используется. Тип EXTENDED:

а) 0,670993000501766*2^(-12192);

б) -0,835496500250883*2^(-12191);

в) 0,835496500250883*2^(-12191); +

г) 0,835496500250883*10^(12191*ln(2)/ln(10));

д) -0,670993000501766*2^(-12192);

е) -0,670993000501766*2^(12192);

ж) 0,835496500250883*10^(-12191*ln(2)/ln(10)); +

з) -0,670993000501766*10^(12192*ln(2)/ln(10));

10). (из 18): В случае алгебраического сложения чисел, представленных в форме с плавающей запятой:

а) их мантиссы должны быть одинаковы;

б) их мантиссы складываются; +

в) их порядки должны быть одинаковы; +

г) их порядки складываются;

д) их порядки вычитаются;

11). (из 18): Найдите сумму двух чисел, представленнях в форме с плавающей запятой. M1=0.1011001, p1=1110; m2=0.10101001, p2=1010:

а) m3=101111001001; p3=1110;

б) m3=0.101111001001; p3=1110; +

в) m3=0.101111001001; p3=1010;

г) m3=0.101011011; p3=1010;

12). (из 18): Укажите правильно реализованный метод деления с восстановлением остатка двух чисел 1794/78 (см. рис. 4.1):

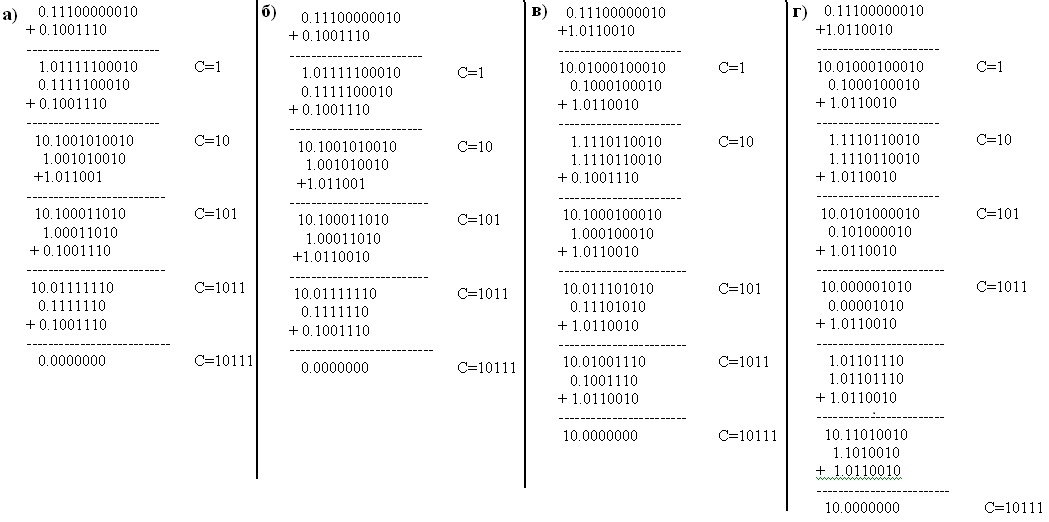Рис. 4.1. Метод деления с восстановлением остатка двух чисел 1794/78.

а) а;

б) б;

в) в; +

г) г;

13). (из 18): Укажите правильно реализованный метод деления без восстановления остатка двух чисел 1710/18 (см. рис. 4.2):

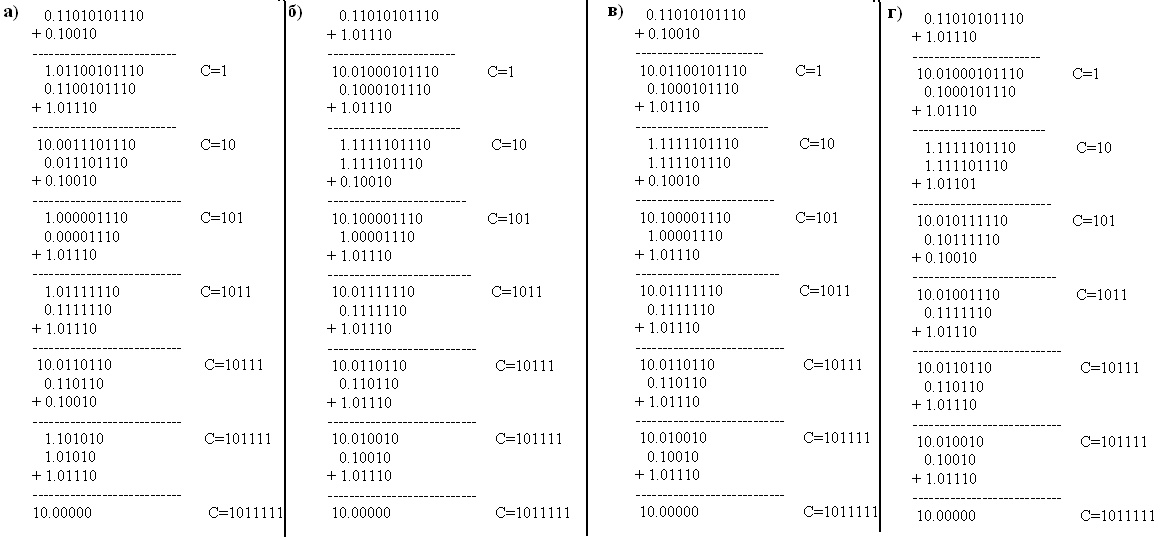Рис. 4.2. Метод деления без восстановления остатка двух чисел 1710/18.

а) а;

б) б; +

в) в;

г) г;

14). (из 18): Укажите правильно реализованный метод деления с восстановлением остатка двух чисел 1044/58 (см. рис. 4.3):

Рис. 4.3. Метод деления с восстановлением остатка двух чисел 1044/58.

а) б;

б) в;

в) а; +

г) г;

15). (из 18): Получить дополнительный код для числа, представленного в Д1-коде, где для знака числа отводится старший разряд. -2973=1.0010 1001 0111 0011:

а) 1.0111 0000 0010 0110;

б) 0.0111 0000 0010 0111;

в) 0. 0111 0000 0010 0101;

г) 1.0111 0000 0010 0111; +

д) 1.0111 0000 0010 0101;

е) 1.0111 0000 0010 1111;

16). (из 18): Получить обратный код для числа, представленного в Д1-коде, где для знака числа отводится старший разряд. 973=0.1001 0111 0011:

а) 1.000000100110;

б) 1.000000100111;

в) 0.111111011001;

г) 1.111111011001;

д) 0.1001 0111 0011; +

17). (из 18): Получить дополнительный код для числа, представленного в Д1-коде, где для знака числа отводится старший разряд. -12785=1.0001 0010 0111 0100 0101:

а) 1.0001 0010 0111 0100 0101;

б) 1.1000 0111 0010 0101 0100;

в) 1.0111 1000 1101 1010 1011;

г) 1.1000 0111 0010 0101 0101; +

д) 0.1000 0111 0010 0101 0101;

18). (из 18): Получить дополнительный код для числа, представленного в Д1-коде, где для знака числа отводится старший разряд. 12785=0.0001 0010 0111 0100 0101:

а) 1.0001 0010 0111 0100 0101;

б) 0.0001 0010 0111 0100 0101; +

в) 1.1000 0111 0010 0101 0100;

г) 1.0111 1000 1101 1010 1011;

д) 0.1000 0111 0010 0101 0101;

е) 1.0001 0010 0111 0100 0111;