Компьютерная логика (тест с ответами): Функции алгебры логики.

24 12

1). (из 13): Ошибки результата при работе цифрового автомата могут быть таких видов:

а) ошибки, возникающие из-за погрешностей в исходных данных; +

б) ошибки, возникающие из-за неправильности выполнения машиной всех операций;

в) ошибки, обусловленные методическими погрешностями; +

г) ошибки, возникающие из-за неисправностей в работе машины; +

д) ошибки, возникающие из-за избыточности в исходных данных;

2). (из 13): Для двух переменных может существовать:

а) 8 различных переключательных функций;

б) 4 различных переключательных функции;

в) 16 различных переключательных функций; +

г) 12 различных переключательных функций;

3). (из 13): Укажите результат сложения по модулю 10 двух десятичных чисел 856 и 94:

а) 950;

б) 840; +

в) 850;

г) 940;

4). (из 13): Укажите логическую операцию, которая была выполнена над двумя двоичными числами (см. рис. 5.1):

Рис. 5.1. Какая логическая операция была выполнена над двумя двоичными числами.

а) была выполнена операция «Штрих Шеффера»;

б) была выполнена операция дизьюнкция;

в) была выполнена операция коньюнкция;

г) была выполнена операция «Стрелка Пирса»; +

5). (из 13): Укажите распределительный закон алгебры логики:

Рис. 5.2. Выберите распределительный закон алгебры логики.

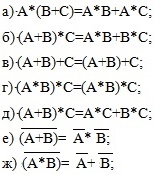
а) а; +

б) б;

в) в;

г) г;

д) д; +

е) е;

ж) ж;

6). (из 13): Дизьюнктивный терм – это:

Рис. 5.3. Выберите дизьюнктивные термы.

а) а;

б) б; +

в) в;

г) г;

д) д;

е) е;

ж) ж; +

з) з; +

7). (из 13): Нормальная конъюнктивная форма (НКФ) – это:

а) дизьюнктивное объединение макстермов, включающее в себя минтермы различных рангов;

б) конъюнктивное объединение минтермов, включающее в себя макстермы различных рангов;

в) конъюнктивное объединение макстермов, включающее в себя макстермы различных рангов; +

г) конъюнктивное объединение макстермов, включающее в себя макстермы одинаковых рангов;

д) дизьюнктивное объединение минтермов, включающее в себя макстермы одинаковых рангов;

8). (из 13): Совершенные нормальные формы:

а) всегда содержат термы только максимального ранга; +

б) являются нормальными каноническими формами представления функции; +

в) всегда содержат термы только минимального ранга;

г) никогда не дают однозначного представления функции;

д) всегда дают однозначное представление функции; +

9). (из 13): Если дана таблица истинности для логической функции, то получить СКНФ можно следующим образом:

а) сформировать макстермы из тех наборов аргументов, на которых функция равна нулю; +

б) сформировать минтермы из тех наборов аргументов, на которых функция равна нулю;

в) сформировать макстермы из тех наборов аргументов, на которых функция равна единице;

г) в каждом наборе над аргументом, равным единице установить знак инверсии; +

д) в каждом наборе над аргументом, равным нулю установить знак отрицания;

10). (из 13): Укажите функции, сохраняющие ноль (см. рис. 5.4):

Рис. 5.4. Функции, сохраняющие ноль.

а) а; +

б) б; +

в) в;

г) г; +

д) д;

е) е;+

11). (из 13): Укажите самодвойственные функции (см. рис. 5.5):

Рис. 5.5. Самодвойственные функции.

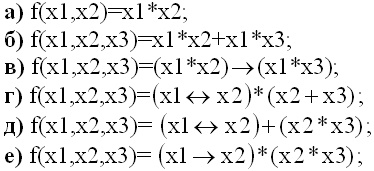
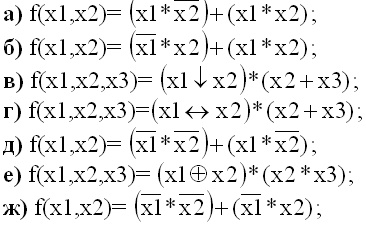
а) а; +

б) б; +

в) в;

г) г;

д) д; +

е) е;

ж) ж;+

12). (из 13): Для того, чтобы система функций являлась базисом необходимо и достаточно, чтобы она содержала хотя бы одну функцию:

а) не сохраняющую ноль; +

б) не сохраняющую единицу; +

в) не являющуюся непрерывной;

г) не являющуюся дискретной;

д) сохраняющую ноль;

е) сохраняющую единицу;

ж) являющуюся линейной;

з) не являющуюся линейной; +

и) не являющуюся монотонной; +

к) не являющуюся самодвойственной; +

л) являющуюся монотонной;

м) являющуюся самодвойственной;

н) являющуюся непрерывной;

о) являющуюся дискретной;

13). (из 13): Аналитическим методом минимизируйте функцию четырёх переменных и укажите правильный результат минимизации (см. рис. 5.6):

Рис. 5.6. Минимизация функции f(A,B,C,D).

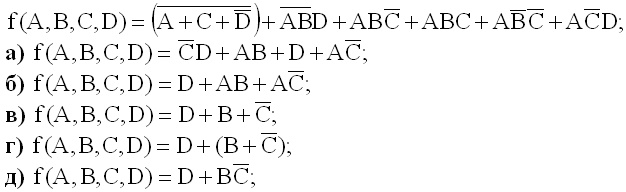
а) а;

б) б; +

в) в;

г) г;

д) д;