Компьютерная логика (тест с ответами): Методы минимизации переключательных функций. Перевод из семеричной системы счисления в четверичную.

36 12

1). (из 14): Метод испытания членов состоит в том, что:

а) если при подстановке выражение тождественно равно единице, то испытываемый член является лишним; +

б) исключают из сокращённой НДФ терм, подставляя в оставшееся выражение такие значения переменных, при которых исключённый член обращается в ноль;

в) если при проверке оказалось, что несколько термов одновременно являются лишними, то исключить их одновременно из выражения ДНФ нельзя. Это можно выполнять лишь поочередно; +

г) если при подстановке выражение тождественно равно нулю, то испытываемый член является лишним;

д) если при проверке оказалось, что несколько термов одновременно являются лишними, то их необходимо исключить одновременно из выражения ДНФ;

е) исключают из сокращённой НДФ терм, подставляя в оставшееся выражение такие значения переменных, при которых исключённый член обращается в единицу; +

ж) если при подстановке выражение тождественно равно единице, то испытываемый член не является лишним;

2). (из 14): Метод Квайна состоит из следующих этапов:

а) провести в СНДФ функции все возможные операции склеивания. В результате этого образуются произведения, содержащие (n-1) букв; +

б) произвести все возможные склеивания членов с (n-1) буквой; +

в) для выражения, в котором уже невозможно провести операции склеивания и поглощения построить матрицу импликант и получить минимальную ДНФ;

г) выполнить все возможные операции поглощения; +

д) для выражения, в котором уже невозможно провести операции склеивания и поглощения построить матрицу импликант и получить сокращённую ДНФ;

е) для выражения, в котором уже невозможно провести операции склеивания и поглощения построить матрицу импликант и получить тупиковые ДНФ;

ж) провести все возможные поглощения членов с (n-1) буквой и вновь выполнить операцию склеивания членов с числом букв, равным (n-2), и т.д. +

3). (из 14): Укажите правильно построенные карты Карно (см. рис. 6.1):

Рис. 6.1. Какие карты Карно правильные.

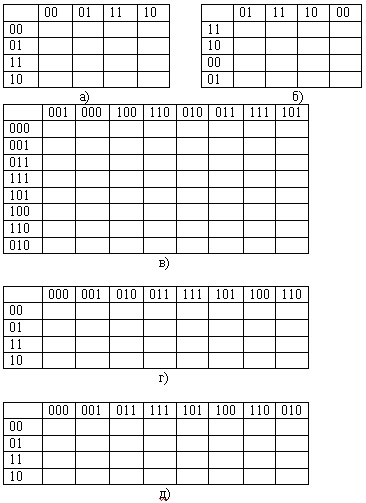
а) а; +

б) б; +

в) в; +

г) г;

д) д; +

4). (из 14): Карту Карно строят имея:

а) НДФ;

б) СНДФ; +

в) сокращённую НДФ;

г) тупиковую НДФ;

д) таблицу истинности; +

5). (из 14): Если в карте Карно объединяются 8 клеток, а сама карта Карно имеет 32 клетки, то полученный терм будет иметь:

а) 1 литерал;

б) 2 литерала; +

в) 3 литерала;

г) 4 литерала;

д) 5 литерал;

6). (из 14): В общем случае с помощью карты Карно можно получить:

а) одну МДНФ;

б) несколько МДНФ; +

в) одну МКНФ;

г) несколько МКНФ; +

д) одну сокращённую КНФ;

е) несколько сокращённых КНФ;

ж) одну СДНФ;

з) несколько СДНФ;

и) одну СКНФ;

к) несколько СКНФ;

7). (из 14): В общем случае сокращённая ДНФ функции:

а) это дизьюнкция всех простых импликантов функции; +

б) получается применением законов склеивания и поглощения к тупиковой ДНФ;

в) получается применением законов склеивания и поглощения к тупиковой КНФ;

г) получается применением метода Квайна к СДНФ; +

д) получается применением законов склеивания и поглощения к СДНФ; +

е) получается применением закона склеивания к СДНФ;

ж) получается применением закона поглощения к СДНФ;

8). (из 14): Алгоритм поиска минимальной ДНФ частично определенной функции включает следующие этапы:

а) выбирают минимальную ДНФ по импликантной матрице, где в столбцах выписаны лишь те конституенты единицы функции f, которые соответствуют полностью определенным единичным наборам; +

б) выбирают минимальную ДНФ по импликантной матрице, где в столбцах выписаны лишь те конституенты нуля функции f, которые соответствуют полностью определенным нулевым наборам;

в) находят любым известным способом сокращенную ДНФ функции, получающуюся доопределением нулями исходной функции f на всех неопределенных наборах;

г) находят любым известным способом сокращенную ДНФ функции, получающуюся доопределением единицами исходной функции f на всех неопределенных наборах; +

д) находят любым известным способом совершенную ДНФ функции, получающуюся доопределением нулями исходной функции f на всех неопределенных наборах;

е) находят любым известным способом СДНФ функции, получающуюся доопределением единицами исходной функции f на всех неопределенных наборах;

9). (из 14): В одноэлементном базисе может участвовать только одна операция:

а) сумма по модулю два;

б) исключающее ИЛИ;

в) стрелка Пирса; +

г) импликация;

д) инверсия;

е) штрих Шеффера; +

ж) И;

з) ИЛИ;

10). (из 14): Операция штрих Шеффера:

а) это отрицание коньюнкции; +

б) это отрицание дизьюнкции;

в) не обладает свойством ассоциативности;

г) обладает свойством ассоциативности;

д) даёт возможность заменить операции дизьюнкции; +

е) даёт возможность заменить операции коньюнкции; +

ж) дуальна по отношению к операции стрелка Пирса; +

11). (из 14): Укажите приоритеты при выполнении логических операций в выражении (от наибольшего к наименьшему):

а) инверсия – дизъюнкция - конъюнкция – импликация – эквивалентность;

б) конъюнкция – дизъюнкция – инверсия – импликация – эквивалентность;

в) инверсия – конъюнкция – дизъюнкция – эквивалентность – импликация;

г) инверсия – конъюнкция – дизъюнкция – импликация – эквивалентность; +

д) конъюнкция – инверсия – дизъюнкция – импликация – эквивалентность;

12). (из 14): Если переходить от МДНФ функции к функции в одноэлементном базисе с операцией штрих Шеффера, то:

а) полученная функция будет минимальной;

б) полученная функция не будет минимальной; +

в) полученная функция будет сокращённой;

г) полученная функция будет совершенной;

д) полученная функция будет тупиковой;

е) полученная функция не будет тупиковой; +

ж) полученная функция не будет сокращённой; +

13). (из 14): Выберите коньюнктивные термы (см. рис. 6.2):

Рис. 6.2. Укажите коньюнктивные термы.

а) +

б)

в)

г) +

д) +

е)

ж)

з)

14). (из 14): Укажите правильно реализованный перевод из семеричной системы счисления в четверичную (см. рис. 6.3) числа 153664:

Рис. 6.3. Укажите правильно реализованный перевод числа из семеричной системы счисления в четверичную.

а) а;

б) б;

в) в; +

г) г;